近日,我校数学与统计学院分析团队教师安庆楠与大连理工大学刘智超在C*-代数的分类问题研究中取得重要突破。C*-代数的分类问题又称为Elliott猜想,其作为算子代数领域中的一个核心问题,是由加拿大科学院院士George A. Elliott教授在1989年提出的。Elliott教授曾在1994年的苏黎世国际数学家大会(ICM)上就该猜想做了45分钟报告。(国际数学家大会由国际数学联盟主办,简称ICM,是全球数学届最高水平的学术会议,素有国际数学“奥运会”之称。首次会议于1897年在瑞士苏黎世召开,已有100多年的历史,一般4年一次。)
Elliott猜想主要分为两部分内容。第一部分:“Elliott单猜想”已经得到了完全解决(可参见2018年和2022年ICM的45分钟报告);而第二部分:“Elliott实秩零猜想”自上世纪90年代起,已近30年未曾有本质性的突破。
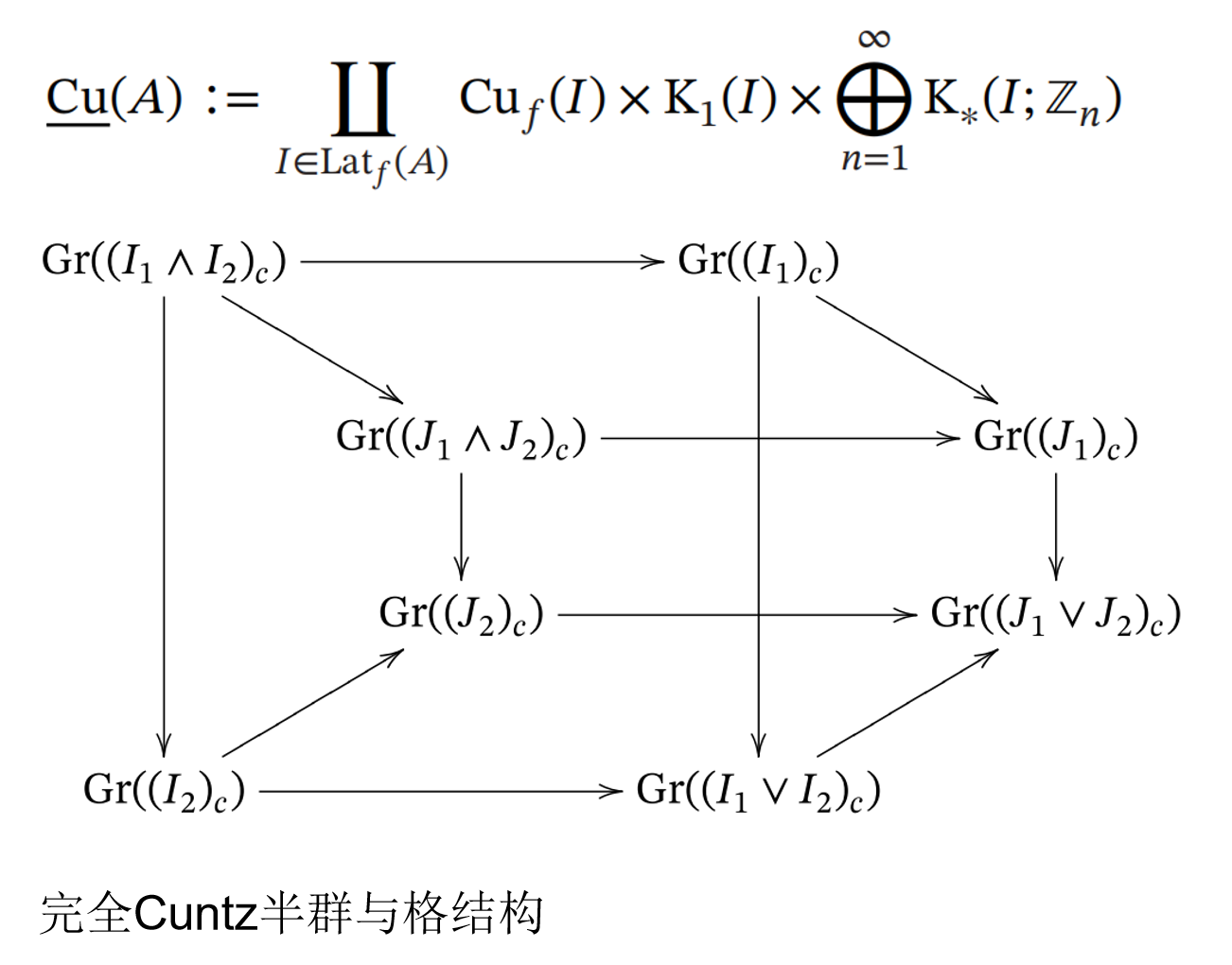
Elliott实秩零猜想认为完全K-理论(total K-theory) 是实秩零稳定秩一C*-代数的完全不变量。我校教师安庆楠与大连理工大学刘智超在国际著名数学期刊《Proceedings of the London Mathematical Society》上发表了题为“Total Cuntz semigroup, extension, and Elliott Conjecture with real rank zero”的研究成果。(该期刊于1865年创刊,是伦敦数学会的旗舰期刊,论文涵盖广泛的数学领域,致力于发表领域内最高质量和重要意义的文章。)两人在该文章中使用扩张理论的工具构造了两个实秩零稳定秩一的C*-代数,他们证明了这两个代数具有相同的完全K-理论,但彼此之间并不同构。这给出了Elliott实秩零猜想的反例。

此外,在这篇文章中,他们还对猜想的正则性条件进行了修正,并使用完全K-理论给出了该修正下基于扩张理论的分类定理;对于不满足新正则性条件的一般情形,他们基于二人在分析学领域国际著名学术期刊《Journal of Functional Analysis》发表的题为“A total Cuntz semigroup for C*-algebras of stable rank one”的文章中构造的完全Cuntz半群这一新的不变量工具分类了从一般扩张中得到的反例代数。
文章链接如下:https://doi.org/10.1112/plms.12595

安庆楠为我校数学与统计学院基础数学学科分析团队讲师,主要从事泛函分析方向的研究和教学工作,相关科研成果在《Proceedings of the London Mathematical Society》《Journal of Functional Analysis》《Journal of Operator Theory》《Science China-Mathematics》等期刊发表。2023年度,获评天元东北中心优秀青年学者。